---

Sampling errors

Sampling errors

General mathematical background

Literature accepts (on the basis of the central limit theorem) that the deviation from actual values of average values calculated from a sample shows normal (or Gauss) distribution, provided the number of elements is large enough (minimum 30-40). That is to say the larger the deviation, the smaller the likelihood of deviation from actual values is, and this relationship follows the following two functions:

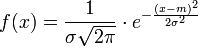
where m is the sample average and σ is the coefficient of variation.

The corresponding general graph shows m located at the middle of the horizontal axis, and the actual value is somewhere on the same axis. The the area below the line in an interval shows the probability (confidence level) of whether or not the interval contains the actual value (confidence interval)

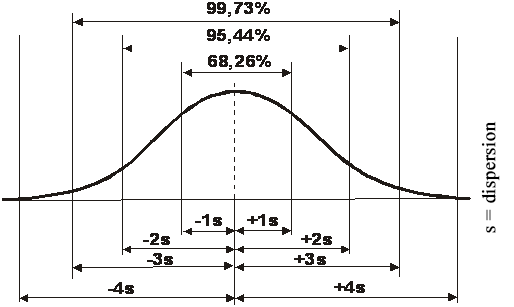
The area below the plotted line in the figure above is 1 (in other words, regardless of how large measurement error is, the probability of which keeps reducing, the plotted line approximates the horizontal axis beyond any limit). It is easy to see that the larger deviation from the sample average we allow, the greater the probability that the confidence interval will contain the actual value. General expectations call for a 95% level of confidence (published tables also include the same margin of error), and the related value is 1.96*s in case of standard normal distribution.

Error of calculating the area inside forest land area and wood volume

To determine sampling error, the following steps need to be taken:

• Calculation of the sample average:

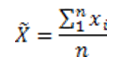
where x_i is the totality of measured values (wood volume, area proportionate to circular disk of cut), and n is the number of these.

• Calculation of sample deviation:

• Determining the confidence interval:

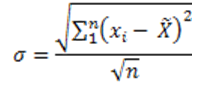
Calculating standard error from the deviation calculated as shown above:

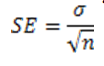
There is a 95% probability that the actual value is inside the ±1.96*SE confidence interval around the calculated value.

The FieldMap InventoryAnalyst software used for data evaluation displays the confidence interval values calculated this way around each calculated value.

Actual sampling and related errors

Samples were taken at the corner points of a grid of equal density covering the whole territory of the country, hence there was no need to set up strata, i.e. the whole country makes up a single stratum. No error emanates from the variability of strata therefore.

Other sources of error to be considered during analysis:

• The density of the sampling grid
• The variability of sampling plots
• Sampling in concentric circles

The density of the sampling grid

It is easy to accept that the sleazier the grid, the larger the sampling error is, and on the other hand, the smaller the forest cover in a country (or in the area studied), the greater the error. The standard error of forest cover can be calculated with the following formula:

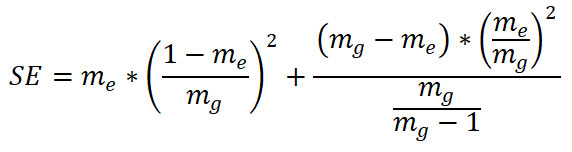
where m_g represents all of the sampling points in the studied area, and m_e is the number of points located on forest land areas. The related confidence interval is:

m_e ±1.96*SE

Specifically, 5355 sampling points located in forest land areas correspond to 2,142,000 hectares of forest land taking the whole territory of the country as the subject matter of analysis. Once the calculations listed above are performed, 23,029 points inside the whole territory of Hungary yield the result where forest land area is between 2,091,739 ha and 2,192,261 ha at 95% probability.

The variability of sampling plots

If the forest studied had fully homogeneous construction, then regardless of the location where trees are measured, the resulting value would be the same. Forests are not like that, but the characteristics (e.g. deviation) of measured samples allow us to make inferences about the error of measured and calculated data. At that point, the calculations shown above need to be performed by substituting x_i with the wood volume calculated for each sampling point and the representative area. Calculations need to take into account potential groupings (such as tree species groups) and the territorial conditions used for filtering sampling points (provided the analysis is not performed for the whole territory/grid). Based on the above, the confidence interval may be "too large" for more uncommon tree species or smaller areas and may even be broader than our calculated values. Whenever that occurs evaluations should be utilised with proper care.

Sampling in concentric circles

As described on the section on methodology, trees with diameters below 20 cm are only recoded inside the 7 m circle, while those between 7 and 12 cm in diameter are only captured in the 3 m circle. These data are "projected" for 500 m² sampling plots, that is to say these trees are taken into account with a weighting that corresponds to the proportional relationships of the areas (3.248 and 17.684). This method rendered sampling much easier and yet the error it created is negligible and plays no role reliability analyses.